High art публикации

Музыку я разъял, как труп.

Поверил Я алгеброй гармонию…

(А.С. Пушкин)

Знаете ли вы, что такое Золотое сечение? Кто такой Витрувианский человек? И что такое гармония?

Божественные пропорции

Начнем с определения. По нему, золотое сечение - соотношение частей, при котором большая часть относится к меньшей также, как все целое относится к большей части. Если перевести золотое сечение на математический язык, оно будет выражено формулой a:b = (a+b):a. Это соотношение равняется бесконечному числу φ («фи»). Для простоты в использовании его значение округляется до 1,62.

Почему же такие пропорции называют золотыми, а столь незвучное число - божественным? Согласно распространенному в наше время мнению, золотое сечение - наиболее совершенное соотношение частей, показатель гармонии, лежащий в основе всего мироустройства. Неужели закон божественной гармонии и вселенской красоты столь прост, что человечество подошло к его разгадке? Не будем спешить с выводами.

Немного истории

Сначала золотое сечение было исключительно геометрическим показателем и занимало лишь античных мыслителей, исследовавших его свойства. Согласно дошедшим до нас источникам, первым о нем заявил александрийский математик Евклид в книге «Начала» (около 300 г. до н. э.). Евклид находит «среднепропорциональное» деление отрезка относительно его краев, при котором весь отрезок относится к бóльшей части, как бóльшая к меньшей. Найденную закономерность ученый использует для построения правильного пятиугольника. Пропорцию изучали также Платон и Пифагор, но никто из них не нарекал ее золотой или «божественной».

Впервые это произошло спустя почти два тысячелетия. В 1835 году математик Мартин Ом, брат знаменитого физика Георга Ома, использовал термин «золотое сечение» в своей книге «Чистая элементарная математика». После этого он распространился - в том числе в кругах теоретиков искусства, размышления которых постепенно оформлялись в науку.

Обозначение сечения золотым, как и его открытие, часто приписывается Леонардо да Винчи. Парадоксально, но ни одного упоминания божественного сечения в дневниках художника мы не находим. Зато в XIX и, особенно, в XX-XXI веках находятся люди, измеряющие произведения Леонардо и других творцов золотым сечением. Своим «фи» они оценивают конструкцию Парфенона, фигуру Венеры Милосской, древнеегипетские рельефы и многое другое. Можно ли утверждать, что древние мастера нарочно отмеряли золотые пропорции? Во всей истории искусства мы знаем лишь несколько примеров, когда художники осознанно экспериментировали с золотым сечением - почти все они относятся к XIX и XX векам. К примеру, русский художник Константин Васильев был в восторге от золотого сечения, как удобного способа разметки холста. Знали о пропорциях в стенах Санкт-Петербургской Академии художеств конца XIX века, где по его принципу создавались академические полотна - хорошие и не очень. Значит принцип "фи" - не панацея?

Золотое сечение в геометрии и в природе

Наверняка, вы не раз встречали схему золотого сечения, наложенную на картины, скульптуры, здания. Как правило, это закручивающаяся спираль – спираль Фибоначчи, носящая имя средневекового итальянского математика Леонардо Фибоначчи (Пизанского).

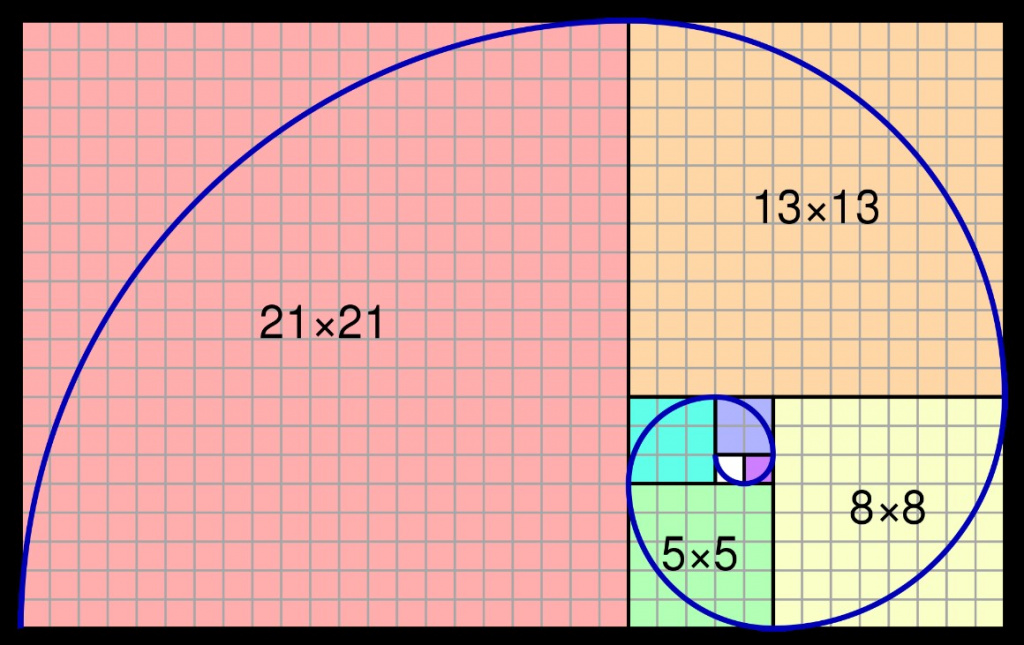
Как показано на картинке, спираль Фибоначчи проходит через квадраты. Сторона каждого следующего квадрата больше стороны предыдущего примерно в 1,62 раза, то есть в числовое значение φ. Например, длина стороны желтого квадрата равняется 8, что в 1,62 раза больше длины стороны зеленого квадрата, равной 5, и так далее. Помимо этого, спираль золотого сечения бесконечно вписывается в прямоугольники, которые, в свою очередь, складываются из двух квадратов и следующего прямоугольника с витком спирали. Площадь прямоугольника относится к площади большего квадрата также, как площадь большего квадрата относится к сумме площадей меньшего квадрата и меньшего прямоугольника, то есть наглядно воплощает золотые пропорции.

Спираль Фибоначчи, как утверждают сторонники золотого сечения, можно встретить в совершенных природных формах. По описанному принципу закручиваются раковины членистоногих, сердцевины некоторых цветов, молекула ДНК, спиральные рукава млечного пути. Возможно ли с точностью до цифр пропорции измерить все это? Также возникает вопрос, есть ли у спирали Фибоначчи преимущество перед архимедовыми спиралями, идеальными и не очень окружностями, треугольниками, гексасферами и иными формами и соотношениями, на которых строится мир?

Упомянув итальянского математика, мы не сказали о его теории роста популяции кроликов и волшебных числах, описанных в книге «Liber Abaci» (1202). Фибоначчи предлагает представить, что изначально имеется одна пара кроликов. В первом месяце у нее рождается два разнополых крольчонка, составляющих одну пару. Во втором месяце родители и их подросшие дети производят на свет по паре – в сумме две новые пары крольчат. В третьем месяце первая пара погибает, а вторая пара и две пары из третьего поколения рождают еще по одной паре кроликов – в сумме три новые пары. В четвертом месяце погибает второе поколение, а все остальные пары производят по паре: в результате чего на свет появляется пять новых пар и так - до бесконечности.

Описав эту закономерность, математик подошел к открытию: числам Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Как относится каждое предыдущее число к следующему? Суммируют ли два предыдущих числа третье, следующее за ними? Да, длинноухие зверьки напомнили о волшебных цифрах – величинах золотого сечения! Взгляните еще раз на квадраты, и вы увидите, что их стороны и есть эти самые величины.

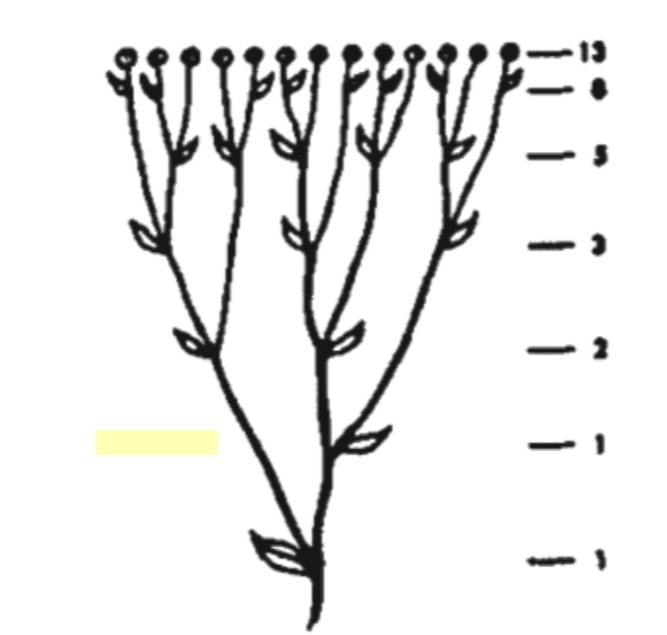
К счастью, в условиях естественного отбора, кролики не смогут плодиться в таких масштабах – иначе они бы вытеснили другие виды. Однако если в реальности такое распространение кроликов невозможно, то где же еще проявляются числа Фибоначчи? Исследователи чисел предлагают поставить вместо пар кроликов новые побеги на ветке. В первый месяц на ветке появляется один побег и так далее. Этот вариант наши зелёные друзья действительно используют, но не так часто. Нужно ли растению знать числа Фибоначчи, чтобы просто расти?

Миф об идеальном человеке

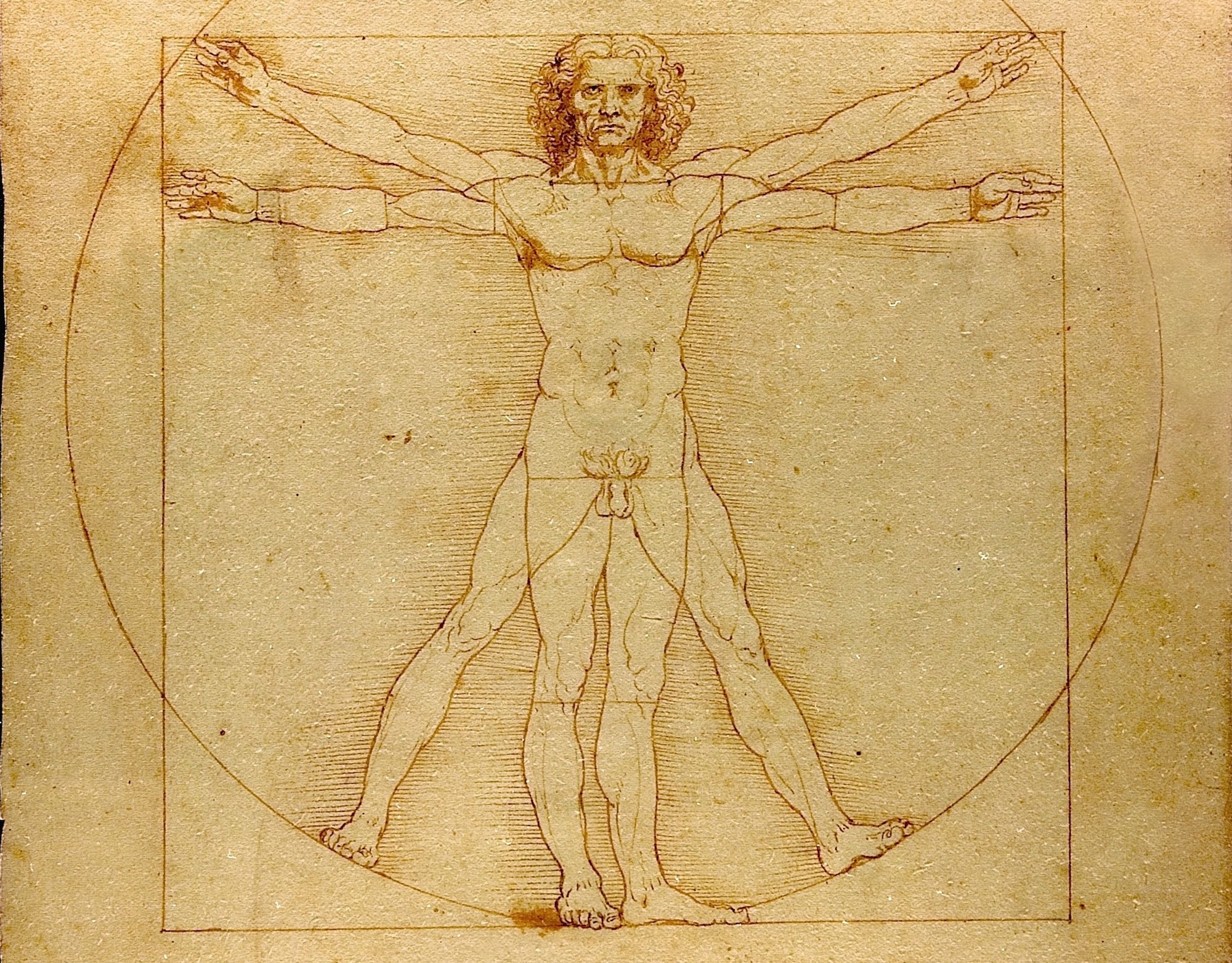
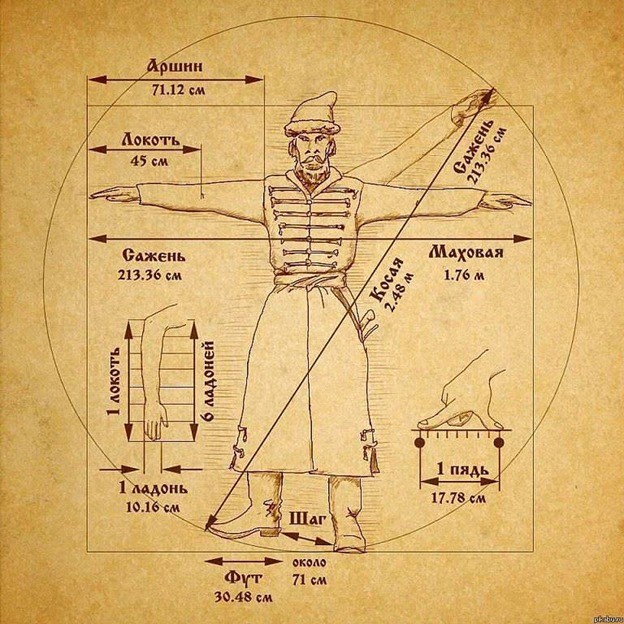
Существует несколько распространенных мифов, связанных с именем Леонардо да Винчи и золотым сечением. Главный из них - «Витрувианский человек». Считается, что рисунок, датированный примерно 1492 годом, воплощает идеальные пропорции человеческого тела, выстроенные по принципу золотого сечения. Знаменитое изображение человека, вписанного в круг и квадрат, является иллюстрацией к книге, посвященной древнеримскому архитектору Витрувию. Витрувий известен своим огромным трудом «Десять книг об архитектуре», где подробно излагает идею строительства архитектурных сооружений по принципам, заложенным в человеческом теле.

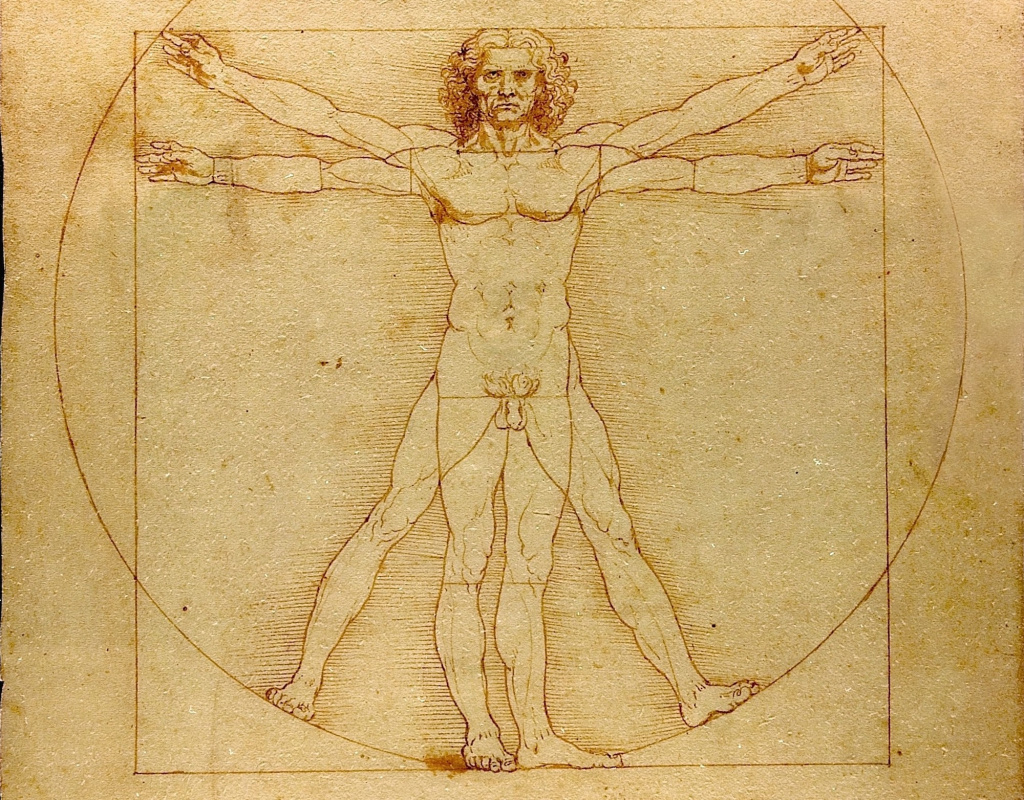
Архитектор посвящает одну из книг тому, как должен выглядеть идеальный человек. Он измеряет рост человека локтями и ладонями (к примеру, высота человека составляет четыре локтя от кончиков пальцев и, соответственно, 24 ладони), а также отмеряет идеальную длину частей его тела относительно его роста (длина руки составляет ⅖ его высоты и тд.). Удивительно, но для того, чтобы объяснить, как строить устойчивые и красивые здания, Витрувий использует простейший способ измерения. Так, не знавшие линеек русские купцы бойко отмеряли ткани локтями - ведь не щуками же это делать, к тому же локоть всегда при тебе. А англичане определяли расстояние пройденными шагами, футами.

Проливает ли Витрувий свет на то, как следовать гармонии? В первой главе первого тома говорится, что идеальный архитектор должен знать не только свое ремесло, но и разбираться в музыке, истории, астрономии, обладать грамотностью. То есть быть человеком, способным "судить обо всем, выполняемом посредством других искусств", быть образованным. Потому что не будучи образованным, человек не увидит гармонию в другом.

Кстати, во всех десяти томах – ни слова о золотом сечении! Соответственно, и «Витрувианский человек» не имеет к нему прямого отношения.

Правда, в рисунке все же находят золотое сечение - оно делит тело человека ровно по линии пупка. Но и здесь при подсчетах вскрываются неточности: пупок мужчины находится не на высоте "фи" (Н : 1,62) а на высоте, полученной из логики членения квадрата (Н : 1,64).

Миф о золотом сечении – «коде да Винчи», был разогрет на почве одноименного романа Дэна Брауна. Бестселлер нулевого десятилетия настолько захватил умы широкой публики, что в сознании людей имя да Винчи окутало флером загадочных чисел – ключей к разгадкам вселенских тайн.

Будет несправедливым сказать, что Леонардо да Винчи никогда сознательно не использовал золотое сечение. Через шесть лет после создания Витрувианского человека он иллюстрирует трактат «Божественная пропорция» известного на тот момент математика Луки Пачоли. В трактате Пачоли изучает наследие Евклида, приводит правила для вычисления объёмов тел с золотыми пропорциями и даже сравнивает их части с христианской Троицей - при этом взгляд автора «математико-космологический». При всей своей любви к золотом сечению, Пачоли даже не думает называть его главной пропорцией – мерилом красоты архитектуры и живописи.

Идеальная женщина Дюрера

Один из главных представителей Северного Возрождения, художник Альбрехт Дюрер, также обратился к Витрувию при создании идеальной женской фигуры. В результате получилась богиня Возмездия на гравюре «Немезида или Большая Фортуна» (1502) - женщина, мягко сказать, на любителя. Неудивительно, что разочаровавшись в Витрувии, Дюрер сам написал четыре книги о пропорциях человеческого тела, в которых описывал красоту и обращался к природе. В конце концов, художник пришел к заключению, что там, где речь идет о формах, на Земле нет никого, кто мог бы судить о том, что такое абсолютно самое прекрасное. "Нет также на земле человека, который мог бы окончательно сказать, какою должна быть прекраснейшая человеческая фигура. Никто не знает этого, кроме одного Бога".

В итоге - о гармонии

Слова Дюрера подтверждают, что золотое сечение - лишь одна из человеческих попыток заключить в числах, схемах, шаблонах изменчивую гармонию. Почему людям нравится искать готовые решения? Потому что это освобождает человека от необходимости мыслить, а мыслить человек не любит.

Значит, золотое сечение не может лежать в основе гениального произведения? Может, если она берётся за точку отсчёта. Не будем забывать, что это лишь условное обозначение и точка отсчёта может быть любой. Гармония не знает превосходных степеней.

Ваша Лиза Чума